THE BASIC FACTS ABOUT WIND ENERGY


logo
<--------------------------------------------------------------------------------------------------------------------------------->

HOW IT WORKS



Any moving object has kinetic energy. In classical mechanics, its amount E in joules is given by the equation E=mv2/2, where m is the mass in kg, and v is the speed in m/sec. Air molecules have mass, and when they are in motion, they contain kinetic energy that can be converted into other forms for practical use.
When molecules hit a surface of any object that is allowed to move, their motion is partially transfered to the moving object. Particularly, in wind turbines the energy is extracted from the air as it moves through the "swept area" of the turbine's blades. During this process the air turns the aerodynamically designed blades, which transfer this harvested energy into a spinning shaft. The shaft is connected to a generator's rotor whose motion makes electricity.

HOW MUCH POWER IS IN THE WIND



The wind energy diagram below illustrates the process of energy transfer. If D is the diameter of the turbine's blades, they intercept the air in the cross-sectional area A=π(D/2)2.
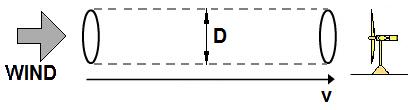
Wind turbine energy transfer diagram
In a time t, the mass of the air that will pass through this area is m=ρ×A×v×t, where ρ is the density of the air (approximately 1.2kg/m3 at sea level).
By combining the above formulas, we can calculate the energy of the air that passes through an area A in a time t: E=ρ×A×v3×t/2

Then power in watts being E per unit time is given by:
P= ρ×A×v3/2

Note that to get the result in watts, all the values in these formulas have to be expressed in SI units (for non-SI units we would need to add some conversion coefficients). We see that power available in the wind is proportional to the cube of its speed and the size of the turbine's blades. If for example, the speed doubles, the available watts increases by a factor of eight.

HOW MUCH ELECTRICITY A TURBINE CAN GENERATE



The above formula for P represents the amount of power in the imaginary tube of the air that flows through the turbine's swept area A. However, only a fraction of this wind power can be actually extracted- there is no way to harvest all of it. If all of air's energy was transfered to the turbine, the air molecules that hit the blades would have to come to a complete stop. This is impossible since for continuous operation since the molecules that already hit the blades need to get out of the way to let the air that is behind them hit the blades. If all the air motion was transferred to the blades, the air would pile up in front of the turbine, and then the wind would have to blow around the turbine. The fact is, the air that hits the blades must keep some speed to move out of the way to allow continuous air flow into the turbine. According to physics, the theoretical limit of wind energy that can be transfered to the shaft is 59.26%. This fact is known as the Betz Limit. In practice, the collection efficiency of commercially manufactured rotors for home use is typically 25% to 45%. Small models for homes tend to have the efficiency at the lower end of this range.

Example. Suppose you have a micro turbine with blade diameter 1 m (about 3 ft) and efficiency 20%. Let's calculate how much electricty it can generate for your home at the air speed 6 m/sec (which is about 13.4 mph).
Rotor swept area: A= π(D/2)2 = 3.14×(1/2)2 = 0.785 m2
Available power in the wind: Pwind= ρ×A×v3/2 = 1.2×0.785×63/2 = 101.7 watt
Then the power that can be extracted at that speed is: Pturbine=0.20×101.7=20.3 watt.


REFERENCES AND ADDITIONAL INFO
Windpower Engineering magazine - design, installation, and maintenance info for the windpower professional; insights to today's wind power issues



<--------------------------------------------------------------------------------------------------------------------------------->